Contact Info

Location Engineering Building | room 332
Phone 435-797-1494
Contact Christian Bolander
Email christian.bolander@usu.edu

Hours

Mon–Thu	10am – 5pm
Fri	10am – 4pm

Drop-Ins Welcome!

Closed weekends and university holidays.

Derivatives

Engineering Context:

Engineers often deal with the study and manipulation of moving objects. They also are involved in finding the maximums and minimums of various scenarios. Derivatives are the exact tool we use to determine these values of max and min as well as speed, velocity, and acceleration.

MAE: An understanding of derivatives is essential to understanding different types of motion. Velocity and acceleration are both rates of change of position over time. Namely, velocity (v) is the derivative of position (s), and acceleration (a) is the derivative of velocity:

\frac{d s}{d t} = v, \frac{d v}{d t} = a

Mechanical engineers are often dealing with moving objects and manipulation of velocity and acceleration, and a strong understanding of derivatives is central to work with dynamic systems.

ECE: In electrical circuits, the relationship between voltage and current is differential, as is the relationship between power and energy. Voltage is the rate of change of electric potential energy per unit charge. Current is the rate of change of electric charge over time. Power is the rate of change of electric energy over time. An understanding of all of these concepts requires a solid understanding of derivatives, rates of change, and derivative relationships.

BENG: Biological engineers often deal with chemical and enzymatic reaction rates. The rate of change of an enzymatic reaction is given by the derivative $\frac{d S}{d t}$ , or change in substrate formation over change in time. Bacterial growth is also modeled with an equation involving derivatives:

\frac{d X}{d t} = μ X

where $X$ is the concentration of bacterial cells and $μ$ is the growth rate.

CEE: Derivatives can be used in analysis of uphill and downhill grades of slopes, such as in construction of roadways. For example, if a hilltop is modeled by the parabolic equation $y (x) = a x^{2} + b x + c$ , the derivative $\frac{d y}{d x}$ of this equation can be used to determine the slope and grade at different points along the hill.

The Essentials

A derivative is a type of mathematical operation that transforms one function into another. It is a way of relating a function to its slope, or in other words to its rate of change, over time. Very few functions have a constant slope, so taking derivatives is very useful for the analysis of nonlinear functions. The process of finding a derivative is called differentiation. A derivative is most frequently notated as $\frac{d y}{d x}$ or $f^{'} (x)$ .

The derivative of a function is the instantaneous rate of change with respect to one of the variables of the function. It can also be said that the derivative shows us the slope of the tangent line at a point along the function:

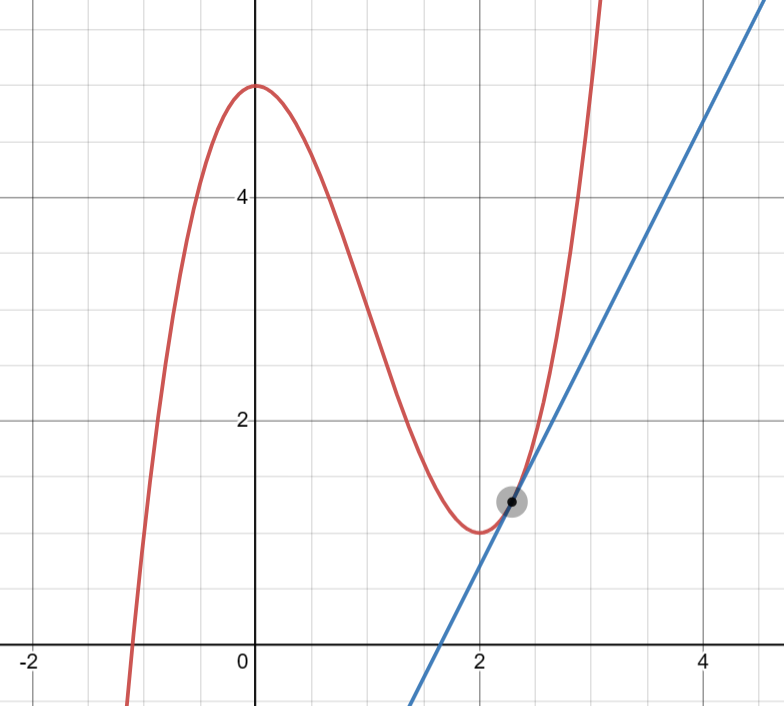
$Tangent Line$

Figure 1: the blue line above is tangent to the graph of $f (x)$ at a point $a$ (in black). The value of this line is equal to the derivative of $f (x)$ at point $a$ .

Thus, a derivative tells us exactly how fast a function is changing at one specific point in time. Mathematically, when you take the derivative of a function, you will end up with another function. For example, the derivative of $f (x) = x^{2}$ is the function $f^{'} (x) = 2 x$ . Plugging in a value of $x$ to this derivative function will then give you the derivative at that specific point. The derivative function at point $x$ has a y-value equal to the slope of the original function at that same point $x$ .

Limit Definition of Derivative at a Point

Definition. Let $f (x)$ be a function defined in an open interval containing the point $a$ . The derivative of $f (x)$ at the point $a$ is denoted by $f^{'} (a)$ or $\frac{d}{d x} (a)$ . Then

f^{'} (a) = lim_{x \to a} \frac{f (x) - f (a)}{x - a}

provided this limit exists.

The derivative may also be found by

f^{'} (a) = lim_{h \to 0} \frac{f (a + h) - f (a)}{h}

Derivative as a Function

Definition. Let $f (x)$ be a function. The derivative function, $f^{'} (x)$ or $\frac{d}{d x} (x)$ , is the function whose domain consist of thos values of $x$ such that the following limit exists:

f^{'} (x) = lim_{h \to 0} \frac{f (x + h) - f (x)}{h}

A Deeper Dive

You can think of a derivative as a local analysis of the relationship between input and output around a certain point of a function. In earlier math classes, we used $\frac{rise}{run}$ to find the slope a function. Finding a derivative uses essentially the same process, but using infinitely small values for rise and run. Since slope of a function is given by $\frac{∆ y}{∆ x}$ or $\frac{rise}{run}$ and since a derivative is thought of as an instantaneous slope, it would make sense that a derivative $\frac{d y}{d x}$ is the slope of an infinitely small interval, with an infinitely small change in $y$ over an infinitely small change in $x$ , as illustrated in the image below:

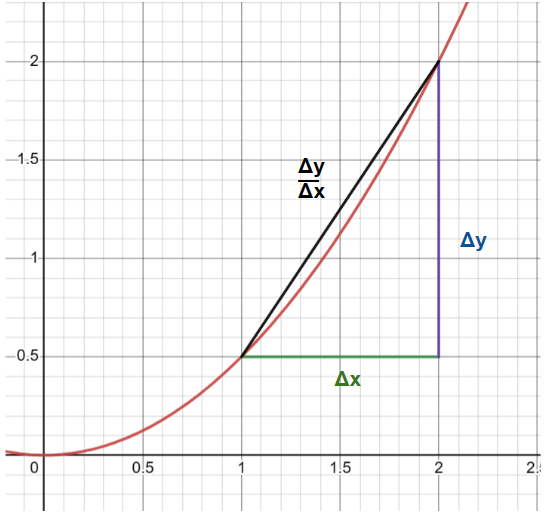
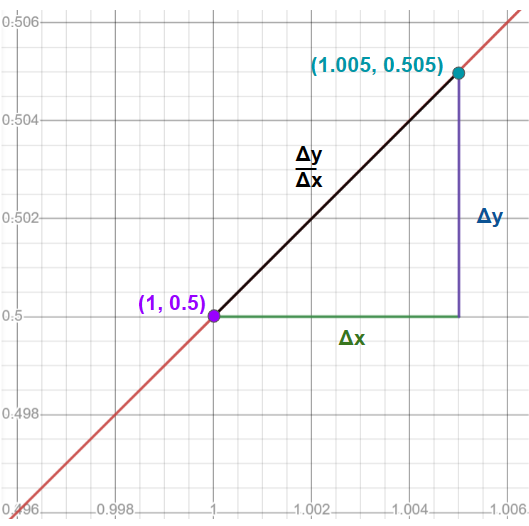
$Normal Derivative Line$ $Zoomed Derivative Line$

Figure 2: The graph $f (x) = \frac{1}{2} x^{2}$ , scaled normally on the left and zoomed in to the point (1,.05) on the right. As you zoom in further to this specific point and look at increasingly small values of $∆ y$ and $∆ x$ , those values will eventually become infinitely small differentials-graph-a $d y$ and $d x$ , and the slope between them the derivative $\frac{d y}{d x}$ at the point (1,0.5).

It's important to note that derivatives and continuity are heavily related. A function $f (x)$ is continuous at the point $x = a$ if the function is differentiable at the point $x = a$ . A function $f (x)$ can also be said to be continuous across its domain if it is also differentiable across its domain.

Often times different notation will be used for derivatives in different circumstances. Below is a limits of all the ways a derivative can be represented:

f^{'} (x) = f^{'} = y^{'} = \frac{d f}{d x} = \frac{d y}{d x} = \frac{d}{d x} (f  (x)) = \frac{d}{d x} (y)

One extremely useful application of derivatives is that of speed, velocity, and acceleration. These three values or measurements are related in a way that uses the derivative. The general form for posision $s$ in some measurement of distance (e.g. feet, meters, mils) as a function of time $t$ (e.g. seconds, minutes, hours) is express

s (t) = a t^{2} + b t + c

Taking the derivative of that function produces the general form of the velocity Function $v (t)$ where velocity is measured in some units such $m / s$ or $mi / hr$ .

v (t) = 2 a t + b

Taking the derivative yet again will produce the general form for the acceleration function $a (t)$ where acceleration is measured in some units such as $m / s^{2}$ .

a (t) = 2 a

Practice

Exercise 1. For $f (x) = x^{2} + 2 x - 15$ find $f^{'} (3)$ using the definition of the derivative.

Solutions:

Exercise 1.

f^{'} (3) = lim_{x \to 3} \frac{x^{2} + 2 x - 15 - {(3)}^{2} + 2 (3) - 15}{x - 3}

f^{'} (3) = lim_{x \to 3} \frac{x^{2} + 2 x - 15 - 0}{x - 3}

f^{'} (3) = lim_{x \to 3} \frac{(x + 5) (x - 3)}{x - 3}

f^{'} (3) = lim_{x \to 3} (x + 5) = 3 + 5 = 8

Derivatives

Engineering Context:

The Essentials

A Deeper Dive

Practice

More Resources